The AWS procedure (Fig 1)

The detection of breakpoints is based on the estimation of a piecewise constant function with the Adaptive Weights Smoothing (AWS) procedure (Polzehl and Spokoiny, 2002): AWS is an iterative, data-adaptive smoothing technique that was designed for smoothing in regression problems involving discontinuous regression function. The regression function is approximated by a simple local constant gaussian model and estimated as a weighted Maximum Likelihood Estimate (MLE), the choice of the weights being completely data-adaptive. The weighted MLE $\hat{\theta}(X_i)=\hat{\theta}_i$ is of the form:

$$\hat{\theta}_i = \underset{\theta \in \Theta}{\textrm{min}} \frac{1}{2\sigma^2}\sum_{j=1}^N w_{ij}(Y_j-\theta)^2$$

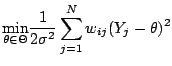The AWS procedure allows the computation of the weights $w_{ij}$ through an iterative procedure: at each iteration $k$, the increase in $h^{(k-1)}$ defines a new larger neighborhood around each $X_i$, which is used to calculate the new MLE of $\theta_i$. For each location $X_i$, the estimation $\theta^{(k-1)}_i$ is improved by computing the new weights taking into account:

• the distance between $X_i$ and $X_j$ in terms of geographical proximity $\rightarrow \boldsymbol{l}_{ij}^{(k)}$

• the distance between $X_i$ and $X_j$ in terms of statistical comparison $\rightarrow \boldsymbol{s}_{ij}^{(k)}$

The new weight $w_{ij}^{(k)}$ is calculated as a function of $K_l\big(\boldsymbol{l}_{ij}^{(k)}\big)K_s\big(\boldsymbol{s}_{ij}^{(k)}\big)$ where kernels $K_s$ and $K_l$ are non-increasing functions and must fulfill $K_s(0)=K_l(0)=1$.

Summary of the AWS procedure:

Initialization:

set all $\theta_i^{(0)}$ to the mean of the $\textrm{log}_2\textrm{-ratio's }$$Y_i$ and all weights $w_{ij}^{(0)}$ to 1

Iteration:

for each location $X_i$:

• Start by looking at its closest neighbors
• Recompute the new weights $w_{ij}^{(k)}$ (in a neighborhood of radius $h^{(k)}$)
• Increase the size of neighborhood $h^{(k)}$ at each step $k$

Stop:

when $h^{(k)}$ is greater than a fixed threshold

Figure 1: Aws results